4.4 ฟังก์ชันเอกซ์โพเนนเชียล
ฟังก์ชันนั้นมีอยู่หลายรูปแบบ แต่ละแบบก็มีการตั้งชื่อไม่เหมือนกัน ฟังก์ชันเอกซ์โพเนนเชียลก็เป็นอีกรูปแบบหนึ่งของฟังก์ชันซึ่งเราจะไปดูว่าฟังก์ชันเอกซ์โพนเนนเชียลนั้นมีรูปแบบอย่างไร ก็ต้องไปดูนิยามของมันครับ ว่านิยามของฟังก์ชันเอกซ์โพเนนเชียลนั้นเป็นอย่างไร อ่านเพิ่มเติม
วันพุธที่ 12 กรกฎาคม พ.ศ. 2560
4.3 ฟังก์ชันกำลังสอง
4.3 ฟังก์ชันกำลังสอง
ฟังก์ชันกำลังสอง คือ ฟังก์ชันที่อยู่ในรูป เมื่อ a,b,c เป็นจำนวนจริงใดๆ และ
เมื่อ a,b,c เป็นจำนวนจริงใดๆ และ  ลักษณะของกราฟของฟังก์ชันนี้ขึ้นอยู่กับค่าของ a , b และ c และเมื่อค่าของ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ อ่านเพิ่มเติม
ลักษณะของกราฟของฟังก์ชันนี้ขึ้นอยู่กับค่าของ a , b และ c และเมื่อค่าของ a เป็นบวกหรือลบ จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ อ่านเพิ่มเติม

ฟังก์ชันกำลังสอง คือ ฟังก์ชันที่อยู่ในรูป
4.2 ฟังก์ชันเชิงเส้น
4.2 ฟังก์ชันเชิงเส้น
ในคณิตศาสตร์ขั้นสูง ฟังก์ชันเชิงเส้น หมายถึง ฟังก์ชันที่เป็น ฟังก์ชันเชิงเส้น มักหมายถึง คณิตศาสตร์ ที่เป็น การสายเส้นตรง ระหว่างสองกลุ่มเวกเตอร์
, โดยที่ M คือ เมตริก
ฟังก์ชัน  จะเป็น การสายเส้นตรง ก็ต่อเมื่อ
จะเป็น การสายเส้นตรง ก็ต่อเมื่อ  เท่านั้น อ่านเพิ่มเติม
เท่านั้น อ่านเพิ่มเติม
 จะเป็น การสายเส้นตรง ก็ต่อเมื่อ
จะเป็น การสายเส้นตรง ก็ต่อเมื่อ  เท่านั้น อ่านเพิ่มเติม
เท่านั้น อ่านเพิ่มเติม4.1 ความสัมพันธ์เเละฟังก์ชัน
4.1 ความสัมพันธ์เเละฟังก์ชัน
คู่อันดับ (Order Pair) เป็นการจับคู่สิ่งของโดยถือลำดับเป็นสำคัญ เช่น คู่อันดับ a, b จะเขียนแทนด้วย (a, b) เรียก a ว่าเป็นสมาชิกตัวหน้า และเรียก b ว่าเป็นสมาชิกตัวหลัง
(การเท่ากับของคู่อันดับ) (a, b) = (c, d) ก็ต่อเมื่อ a = c และ b = d
ผลคูณคาร์ทีเชียน (Cartesian Product) ผลคูณคาร์ทีเซียนของเซต A และเซต B คือ เซตของคู่อันดับ (a, b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B
สัญลักษณ์ ผลคูณคาร์ทีเซียนของเซต A และเซต B เขียนแทนด้วย A x B
หรือ เขียนในรูปเซตแบบบอกเงื่อนไขจะได้ว่า
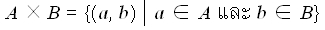 อ่านเพิ่มเติม
อ่านเพิ่มเติม
หรือ เขียนในรูปเซตแบบบอกเงื่อนไขจะได้ว่า
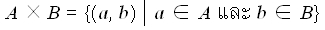 อ่านเพิ่มเติม
อ่านเพิ่มเติม3.3 สมบัติของจำนวนจริงเกี่ยวกับการบวกเเละการคูณ
3.3 สมบัติของจำนวนจริงเกี่ยวกับการบวกเเละการคูณ
สมบัติการบวกในระบบจำนวนจริง กำหนด a, b, c เป็นจำนวนจริงใดๆ
1. สมบัติปิดการบวก a + b เป็นจำนวนจริง
2. สมบัติการสลับที่ของการบวก a + b = b + c
3. สมบัติการเปลี่ยนกลุ่มการบวก a + ( b + c) = ( a + b ) + c
4. เอกลักษณ์การบวก 0 + a = a = a + 0
นั่นคือ ในระบบจำนวนจริงจะมี 0 เป็นเอกลักษณ์การบวก
5. อินเวอร์สการบวก a + ( -a ) = 0 = ( -a ) + a
นั่นคือ ในระบบจำนวนจริง จำนวน a จะมี -a เป็นอินเวอร์สของการบวก อ่านเพิ่มเติม
สมบัติการบวกในระบบจำนวนจริง กำหนด a, b, c เป็นจำนวนจริงใดๆ
1. สมบัติปิดการบวก a + b เป็นจำนวนจริง
2. สมบัติการสลับที่ของการบวก a + b = b + c
3. สมบัติการเปลี่ยนกลุ่มการบวก a + ( b + c) = ( a + b ) + c
4. เอกลักษณ์การบวก 0 + a = a = a + 0
นั่นคือ ในระบบจำนวนจริงจะมี 0 เป็นเอกลักษณ์การบวก
5. อินเวอร์สการบวก a + ( -a ) = 0 = ( -a ) + a
นั่นคือ ในระบบจำนวนจริง จำนวน a จะมี -a เป็นอินเวอร์สของการบวก อ่านเพิ่มเติม
3.2 จำนวนจริง
3.2 จำนวนจริง
มีหลักเกณฑ์ในการแบ่งจำนวนจริงอยู่หลายเกณฑ์ เช่น จำนวนตรรกยะ หรือ จำนวนอตรรกยะ; จำนวนพีชคณิต (algebraic number) หรือ จำนวนอดิศัย; และ จำนวนบวก จำนวนลบ หรือ ศูนย์
จำนวนจริงแทนปริมาณที่ต่อเนื่องกัน โดยทฤษฎีอาจแทนได้ด้วยทศนิยมไม่รู้จบ และมักจะเขียนในรูปเช่น 324.823211247… จุดสามจุด ระบุว่ายังมีหลักต่อ ๆ ไปอีก ไม่ว่าจะยาวเพียงใดก็ตาม
การวัดในวิทยาศาสตร์กายภาพเกือบทั้งหมดจะเป็นการประมาณค่าสู่จำนวนจริง การเขียนในรูปทศนิยม (ซึ่งเป็นจำนวนตรรกยะที่สามารถเขียนเป็นอัตราส่วนที่มีตัวส่วนชัดเจน) ไม่เพียงแต่ทำให้กระชับ แต่ยังทำให้สามารถเข้าใจถึงจำนวนจริงที่แทนได้ในระดับหนึ่งอีกด้วย อ่านเพิ่มเติม
2.2 การให้เหตุผลเเบบนิรนัย
2.2 การให้เหตุผลเเบบนิรนัย
 การให้เหตุผลแบบนิรนัย (อังกฤษ: Deductive reasoning) หรือ การให้เหตุผลจากบนลงล่าง (อังกฤษ: top-down logic) เป็นการนำความรู้พื้นฐานซึ่งอาจเป็นกฎ ข้อตกลง ความเชื่อ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อน และยอมรับว่าเป็นความจริงเพื่อหาเหตุผลนำไปสู่ข้อสรุป เป็นการอ้างเหตุผลที่มีข้อสรุปตามเนื้อหาสาระที่อยู่ภายในขอบเขตของข้ออ้างที่กำหนด อ่านเพิ่มเติม
การให้เหตุผลแบบนิรนัย (อังกฤษ: Deductive reasoning) หรือ การให้เหตุผลจากบนลงล่าง (อังกฤษ: top-down logic) เป็นการนำความรู้พื้นฐานซึ่งอาจเป็นกฎ ข้อตกลง ความเชื่อ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อน และยอมรับว่าเป็นความจริงเพื่อหาเหตุผลนำไปสู่ข้อสรุป เป็นการอ้างเหตุผลที่มีข้อสรุปตามเนื้อหาสาระที่อยู่ภายในขอบเขตของข้ออ้างที่กำหนด อ่านเพิ่มเติม
 การให้เหตุผลแบบนิรนัย (อังกฤษ: Deductive reasoning) หรือ การให้เหตุผลจากบนลงล่าง (อังกฤษ: top-down logic) เป็นการนำความรู้พื้นฐานซึ่งอาจเป็นกฎ ข้อตกลง ความเชื่อ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อน และยอมรับว่าเป็นความจริงเพื่อหาเหตุผลนำไปสู่ข้อสรุป เป็นการอ้างเหตุผลที่มีข้อสรุปตามเนื้อหาสาระที่อยู่ภายในขอบเขตของข้ออ้างที่กำหนด อ่านเพิ่มเติม
การให้เหตุผลแบบนิรนัย (อังกฤษ: Deductive reasoning) หรือ การให้เหตุผลจากบนลงล่าง (อังกฤษ: top-down logic) เป็นการนำความรู้พื้นฐานซึ่งอาจเป็นกฎ ข้อตกลง ความเชื่อ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อน และยอมรับว่าเป็นความจริงเพื่อหาเหตุผลนำไปสู่ข้อสรุป เป็นการอ้างเหตุผลที่มีข้อสรุปตามเนื้อหาสาระที่อยู่ภายในขอบเขตของข้ออ้างที่กำหนด อ่านเพิ่มเติม
2.1 การให้เหตุเเบบอุปนัย
2.1 การให้เหตุเเบบอุปนัย
 การให้เหตุผลแบบอุปนัย (อังกฤษ: Inductive reasoning) หรือ การให้เหตุผลจากล่างขึ้นบน (อังกฤษ: bottom-up logic) เป็นวิธีการสรุปผลมาจากการค้นหาความจริงจากการสังเกตหรือการทดลองหลายครั้ง แล้วนำมาสรุปเป็นความรู้แบบทั่วไป อ่านเพิ่มเติม
การให้เหตุผลแบบอุปนัย (อังกฤษ: Inductive reasoning) หรือ การให้เหตุผลจากล่างขึ้นบน (อังกฤษ: bottom-up logic) เป็นวิธีการสรุปผลมาจากการค้นหาความจริงจากการสังเกตหรือการทดลองหลายครั้ง แล้วนำมาสรุปเป็นความรู้แบบทั่วไป อ่านเพิ่มเติม
 การให้เหตุผลแบบอุปนัย (อังกฤษ: Inductive reasoning) หรือ การให้เหตุผลจากล่างขึ้นบน (อังกฤษ: bottom-up logic) เป็นวิธีการสรุปผลมาจากการค้นหาความจริงจากการสังเกตหรือการทดลองหลายครั้ง แล้วนำมาสรุปเป็นความรู้แบบทั่วไป อ่านเพิ่มเติม
การให้เหตุผลแบบอุปนัย (อังกฤษ: Inductive reasoning) หรือ การให้เหตุผลจากล่างขึ้นบน (อังกฤษ: bottom-up logic) เป็นวิธีการสรุปผลมาจากการค้นหาความจริงจากการสังเกตหรือการทดลองหลายครั้ง แล้วนำมาสรุปเป็นความรู้แบบทั่วไป อ่านเพิ่มเติม
1.4 ยูเนียน อินเตอร์เซกขันเเละคอมพลีเมนต์ของเชต
1.4 ยูเนียน อินเตอร์เซกขันเเละคอมพลีเมนต์ของเชต
ยูเนียน (Union)
ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B
อินเตอร์เซกชัน (Intersection)
อินเตอร์เซกชัน (Intersection) มีนิยามคือ เซต A อินเตอร์เซกชันเซต B คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B
คอมพลีเมนต์ (Complements)
คอมพลีเมนต์ (Complements) มีนิยามคือ ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’ อ่านเพิ่มเติม
1.3 สับเซตเเละเพาเวอร์เซต
1.3 สับเซตเเละเพาเวอร์เซต
สับเซต (Subset)
ถ้าสมาชิกทุกตัวของ A เป็นสมาชิกของ B แล้ว จะเรียกว่า A เป็นสับเซตของ B จะเขียนว่า
เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B
เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B
ถ้าสมาชิกบางตัวของ A ไม่เป็นสมาชิกของ B จะเรียกว่า A ไม่เป็นสับเซตของ B
เซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B
เซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B
เพาเวอร์เซต (Power Set)
คำว่า เพาเวอร์เซต เป็นคำศัพท์เฉพาะ ซึ่งใช้เป็นชื่อเรียกเซตเซตหนึ่งที่เกี่ยวข้องกับเรื่องสับเซต
เพาเวอร์เซตของ A เขียนแทนด้วย P(A)
P(A) คือเซตที่มีสับเซตทั้งหมดของ A เป็นสมาชิก อ่านเพิ่มเติม
1.2 เอกภพสัมพัทธ์
1.2 เอกภพสัมพัทธ์
 เอกภพสัมพัทธ์ คือ เซตที่กำหนดขอบเขตของสิ่งที่ต้องการศึกษา ซึ่งถือว่าเป็นเซตที่ใหญ่ที่สุด โดยมีข้อตกลงว่า ต่อไปจะกล่าวถึงสมาชิกของเซตนี้เท่านั้น จะไม่มีการกล่าวถึงสิ่งใดที่นอกเหนือไปจากสมาชิกของเซตที่กำหนดขึ้นนี้ โดยทั่วไปนิยมใช้สัญลักษณ์ U แทนเอกภพสัมพัทธ์ อ่านเพิ่มเติม
เอกภพสัมพัทธ์ คือ เซตที่กำหนดขอบเขตของสิ่งที่ต้องการศึกษา ซึ่งถือว่าเป็นเซตที่ใหญ่ที่สุด โดยมีข้อตกลงว่า ต่อไปจะกล่าวถึงสมาชิกของเซตนี้เท่านั้น จะไม่มีการกล่าวถึงสิ่งใดที่นอกเหนือไปจากสมาชิกของเซตที่กำหนดขึ้นนี้ โดยทั่วไปนิยมใช้สัญลักษณ์ U แทนเอกภพสัมพัทธ์ อ่านเพิ่มเติม
 เอกภพสัมพัทธ์ คือ เซตที่กำหนดขอบเขตของสิ่งที่ต้องการศึกษา ซึ่งถือว่าเป็นเซตที่ใหญ่ที่สุด โดยมีข้อตกลงว่า ต่อไปจะกล่าวถึงสมาชิกของเซตนี้เท่านั้น จะไม่มีการกล่าวถึงสิ่งใดที่นอกเหนือไปจากสมาชิกของเซตที่กำหนดขึ้นนี้ โดยทั่วไปนิยมใช้สัญลักษณ์ U แทนเอกภพสัมพัทธ์ อ่านเพิ่มเติม
เอกภพสัมพัทธ์ คือ เซตที่กำหนดขอบเขตของสิ่งที่ต้องการศึกษา ซึ่งถือว่าเป็นเซตที่ใหญ่ที่สุด โดยมีข้อตกลงว่า ต่อไปจะกล่าวถึงสมาชิกของเซตนี้เท่านั้น จะไม่มีการกล่าวถึงสิ่งใดที่นอกเหนือไปจากสมาชิกของเซตที่กำหนดขึ้นนี้ โดยทั่วไปนิยมใช้สัญลักษณ์ U แทนเอกภพสัมพัทธ์ อ่านเพิ่มเติม
1.1 เซต
1.1 เซต
| ซตว่าง (Empty Set) | คือ เซตที่ไม่มีสมาชิกเลย เขียนแทนด้วย { } หรือ  (phi) เช่น (phi) เช่น เซตของจำนวนเต็มที่อยู่ระหว่าง 1 กัน 2 เซตของจำนวนเต็มที่อยู่ระหว่าง 1 กัน 2 เซตของสระในคำว่า "อรวรรณ" เซตของสระในคำว่า "อรวรรณ" |
| เซตจำกัด (Finite Set) | คือ เซตที่มีจำนวนสมาชิกเท่ากับจำนวนเต็มบวก หรือ ศูนย์ เช่น  มีจำนวนสมาชิกเป็น 0 มีจำนวนสมาชิกเป็น 0 {1, 2, 3, ...,100} มีจำนวนสมาชิกเป็น 100 {1, 2, 3, ...,100} มีจำนวนสมาชิกเป็น 100 |
| เซตอนันต์ (Infinite Set) | คือ เซตที่ไม่ใช่เซตจำกัด ไม่สามารถบอกจำนวนสมาชิกได้ เช่น เซตของจำนวนเต็มบวก {1, 2, 3, ...} เซตของจำนวนเต็มบวก {1, 2, 3, ...} เซตของจุดบนระนาบ อ่านเพิ่มเติม เซตของจุดบนระนาบ อ่านเพิ่มเติม |
สมัครสมาชิก:
ความคิดเห็น (Atom)




